Dynamic Segment Trees

Dynamic Segment Trees

Dynamic Segment Trees. Here we go.

Problem Statement

You are given the value of N (size of the array initialized to 0) and Q queries to process online

1. 1 P V
   Put value V at position P.
2. 2 L R
   Output the sum of values from L to R.

Constraints:
1<=N<=10^18
Q<=10^5
1<=L<=R<=N

Queries are online
L=(previousAnswer+L)%N+1;
R=(previousAnswer+R)%N+1;
Examples:

Input :

5 5
1 2 3
1 1 4
1 3 5
1 4 7
2 3 4 

Output :

12

Input :

3 2
1 1 1
1 2 2
1 3 3 

Output :

0

Why we need Dynamic Segment trees. let’s dive deep into it.

Let’s solve the problem bit by bit. At first, consider low constraints and offline queries.
This can be done simply by using a Segment Tree or a Fenwick/binary Indexed Tree.
A standard problem for segment trees.
but the problem occurs when you get high constraints.
Like when 1<=N<=10^18.
this much size can't be allocated as an array
also one may propose a solution using co-ordinate compression. As queries Q are less than 10^5.
we can sort the array of queries and then use the hash map to assign a number to every value.
in this way problem with the constraints is resolved, we can compress the intervals to <=10^5, and now we can use a simple segment/BIT to store data.
But, what if you can't use coordinate compression,
what if the question asks you online queries. You cant store the queries now.

Here comes the idea of Dynamic Segment Trees.

It is not a new data structure. It is just implementing a segment tree with existing data structures.
“Just create a node when you need it”.
Instead of creating an array for the segment tree use node to represent Intervals.
structure of a node can be:

01 02 03 04 05 06 07 08 09 10 11 12

//Struct node struct Node {     long long value;     struct Node * L, * R; }; struct Node * getnode() {     struct Node * temp = new struct Node;     temp -> value = 0;     temp -> L = NULL;     temp -> R = NULL;     return temp; }

The structure is the same as a BST. we are storing node’s value and 2 pointers pointing to the left and right node.
The Interval of the root is from(1, N), the interval of its left child will be (1, N/2),
and for the right child, interval will be (N/2 + 1, N).
Similarly, for every node, we can calculate the interval it is representing.
let’s suppose the Interval of the current node is (L, R).
The Interval of its children are: (L, (L+R)/2 ) and ( (L+R)/2+1 , R).
It is a regular segment tree just implement a bit differently.
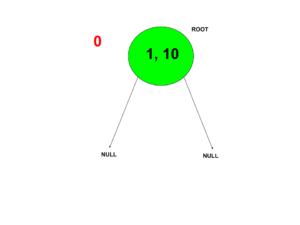
We have a root which contains a complete interval (1,10^18).
if we have to make an update at position 1.
we have to create that node.
Like a regular segment tree complexity of Update and Query is Log(N).
where N is the maximum value of the interval.
But here there’s no requirement of a build() function as we are only creating some of the nodes as per the requirement.
Moreover, If you want to make the following operations:

1. Point update:: whenever you get NULL at the required interval, create a new node.
2. Point Updates:: whenever there’s NULL at a required Interval just return 0, there’s no need of creating new nodes.
3. Range updates:: Keep Making new nodes until required interval.

All tasks have a worst-case complexity of:: O(log(n)).
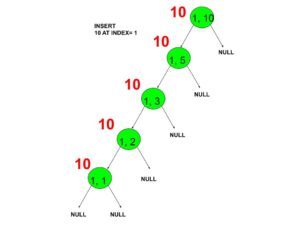
Suppose N is 10 and operations are as follows.

1. insert 10 at 1.
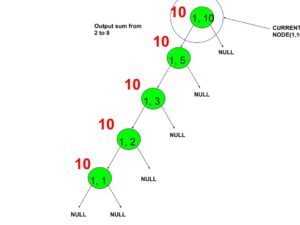
2. output value of indexes from 2 to 8.
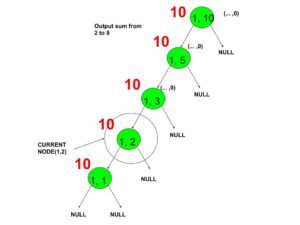
3. insert 3 at 5.
4. output value of indexes from 3 to 6.

Let’s jump right into diagrammatic illustrations.

1. Insert 10 at 1 creating a new node until you get required interval

2. The output value of indexes from 2 to 8.


3. Insert 3 at 5 by creating a new node.

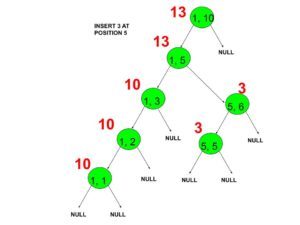
Let’s define some terms:
Node’s interval: It is the interval the node is representing.
Required interval: Interval for which the sum is to calculate.
Required index: Index at which Update is required.

Here’s the algorithm::

1. Query

1. Start with the root node
2. if the node is a NULL entry or interval at that node doesn’t overlap with
   the required interval then return 0
3. If interval at the node completely overlaps with the required interval then return the value stored at the node.
4. Else, if the interval at the node overlaps partially with the required interval then descend into its children by going back to step 2 for both of its children as root.
5. if step 4 is true then return the sum of the values returned by its children.

2. Point Update

1. Start with the root node
2. if the interval at the node doesn't overlap with the required index then return
3. if the node is a NULL entry then create a new node with appropriate interval and descend into that node by going back to step 2 for the child.
4. if both intervals are equal and are equal to the index at which the value is to be stored then store the value into that node’s value.
5. Else, if interval at the node overlaps partially with the required index then descend into its children by going back to step 2.
6. if step 5 is true then update the value at that node as the sum of the values returned by its children.

Let’s look at some C++ source code for the implementation.

01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78

#include <bits/stdc++.h> using namespace std; struct Node {     //structure of the node     long long value;     struct Node * L, * R; }; struct Node * getnode() {     //return the newly fromed node     struct Node * temp = new struct Node;     temp -> value = 0;     temp -> L = NULL;     temp -> R = NULL;     return temp; } struct Node * root; void UpdateHelper(struct Node * curr, long long index, long long L, long long R, long long val) {     // if index is not overlapping with index     if (L > index || R < index) return;     // if index is completely overlapping with index     if (L == R && L == index) {     // change value of node to the given value         curr -> value = val;         return;     }     long long mid = L - (L - R) / 2;     long long sum1 = 0, sum2 = 0;     if (index <= mid) {     // if index is in the left part     // create a new node if it is null         if (curr -> L == NULL) curr -> L = getnode();         UpdateHelper(curr -> L, index, L, mid, val);     } else {     // if index is in the right part         if (curr -> R == NULL) curr -> R = getnode();         UpdateHelper(curr -> R, index, mid + 1, R, val);     }     if (curr -> L) sum1 = curr -> L -> value;     if (curr -> R) sum2 = curr -> R -> value;     // store the sum of its children into the node's value     curr -> value = sum1 + sum2;     return; } long long queryHelper(struct Node * curr, long long a, long long b, long long L, long long R) {     // return 0 if it is null     if (curr == NULL) return 0;     // if index is not overlapping with index     if (L > b || R < a) return 0;     // if index is completely overlapping with index     if (L >= a && R <= b) return curr -> value;     long long mid = L - (L - R) / 2;     // return the sum of values stored at node's children     return queryHelper(curr -> L, a, b, L, mid) + queryHelper(curr -> R, a, b, mid + 1, R); } long long query(int L, int R) {     return queryHelper(root, L, R, 1, 10); } void update(int index, int value) {     UpdateHelper(root, index, 1, 10, value); } int main() {     int n, q;     n = 10;     q = 4;     root = getnode();     update(1, 10);     update(3, 5);     cout << query(2, 8) << endl;     // 5     cout << query(1, 10) << endl;     // 15     return 0; }

the

NOTE: Here we are only focusing on the BST implementation.
There is another version of the BIT which is Implemented as Tries.
I like to call this implementation of a BIT as “Dynamic Binary Indexed Tree”.
Also, this Dynamic BIT is easy to implement and does both update and query in O(length of number).
Let’s leave that for some another article.